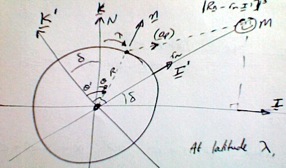
Figure 1: Earth (left) and Moon (top-right)
At any point on the Earth, the Moon will exert a gravitational pull. This acceleration (the force per unit mass) is given by Newton's Law of Gravitation:
`a = F/m = - (G M_"moon" m)/(r^2) 1/m = - mu_m/r^2` (1)
or as a vector:
`ul a = - mu_m/(|ul r|^3) ul r`
where `mu_m` is the "gravitational mass" of the Moon ` = GM_"moon"`, and `ul r` is the position vector of the point on Earth, relative to the Moon.

Figure 1: Earth (left) and Moon (top-right)
The sketch in Fig. 1 shows a view of the Earth from the side, with the equator horizontal, and such that the Moon is in the plane of the paper. The Moon moves roughly in the eliptic (the same plane in which the Sun and the other planets appear to move), so at any particular time it will be above or below the equator, at some angle of declination `delta`.
The Moon's declination will be equal to the Sun's once a lunar month, at the New Moon, because at this time the Moon and Sun are in the same direction. Over the month, the Moon's declination will move up and down between the maximum and minimum of ±23.5 degrees (the Earth's tilt).
With the unit vectors shown,
`ul r = R ul n - r_m ul I'`
so the acceleration felt at the point on the surface is
`ul a = -mu_m (R ul n - r_m ul I')/([R^2 - 2 r_m R sin(theta') + r_m^2]^(3//2))`
Defining `alpha = R//r_m` and `a_0 = mu_m//r_m^2` (i.e. the acceleration felt by the Earth overall, acting at its centre of gravity), then dividing through by `r_m^2` gives
`ul a = -a_0 (alpha ul n - ul I') [alpha^2 - 2 alpha sin(theta') + 1]^(-3//2)`(2)
This can be evaluated numerically, but to see roughly what is happening the equation can be simplified by assuming that `alpha` is small (it is approximately `10^-2`) and using the binomial theorem:
`[alpha^2 - 2 alpha sin(theta') + 1]^(-3//2) ~~ [1 - 2 alpha sin(theta')]^(-3//2) ~~ 1 + 3 alpha sin(theta')`
so `ul a ~~ -a_0 (alpha ul n - ul I' - 3 alpha sin(theta') ul I')`
Because the whole Earth is in free-fall towards the Moon (they are orbiting each other), with acceleration `ul a_0 = a_0 ul I'`, we cannot observe this part of the acceleration. So the measurable acceleration is just:
`ul a"*" ~~ a_0 [3 alpha sin(theta') ul I' - alpha ul n ]`
The component of this in the downwards direction (i.e. `-ul n`) is:
`a_d = ula"*" * (-uln) ~~ a_0 alpha [1 - 3 sin^2(theta')]`(3)
Finally, to see how this varies for a particular location on Earth, consider a point with colatitude `lambda`. As the Earth rotates through an angle `psi` around its axis, the angle `theta` from the Earth's axis will vary as `sin theta = sin lambda cos psi`. The accelerations found above are in terms of the angle `theta'`, given by `theta' = theta + delta`. Putting all of this together, the vertical acceleration (as a fraction of the 'normal' gravity) for three positions of the Moon is plotted below:

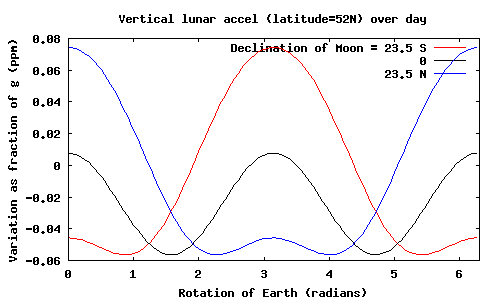
The constant downwards acceleration `a_0 alpha` which appears in (3) seemed to me at first to be wrong: how can the Moon produce a force which is sometimes towards it, sometimes away from it? Actually it is just because the point where the vertical acceleration is zero is not at `theta' = 0`, because the tangent between the Moon and the Earth's surface is at `theta' > 0`.
See also the results of evaluating (2) directly.