The gravitational acceleration felt by a point on Earth due to the Moon may be derived to be:
`ul a = -a_0 (alpha ul n - ul I') [alpha^2 - 2 alpha sin(theta') + 1]^(-3//2)`(2)
where `alpha = "radius of Earth"//"distance to Moon"` and `a_0 = GM//r_m^2` = acceleration of Earth acting at its centre.
As with the simplified analysis, we do not observe the overall acceleration `ula_0`, so the measurable acceleration is
`ula"*" = (-a_0)/eta [alpha uln + (eta - 1)ulI']`
where `eta = [alpha^2 - 2 alpha sin(theta') + 1]^(3//2)`, and `sin(theta'-delta) = sin lambda cos psi`.
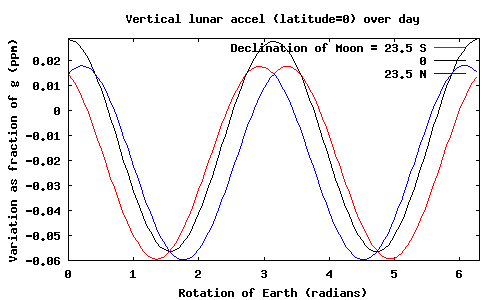
The vertical acceleration (as a fraction of 'normal' gravity) for three positions of the Moon is plotted below, both on the equator and at 52N:

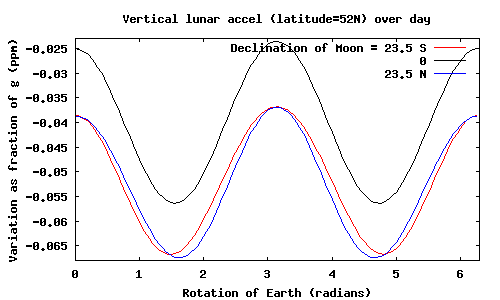
These results seem to disagree with the simplest method.
See also the results of the simplified analysis.