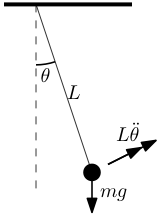

We can find the period of a simple pendulum (figure, right) as follows. Taking `F=ma` in the tangential direction gives:
`m L ddot theta = - mg sin theta` (1)
For small amplitude swinging, we can use the small angles approximation `sin theta ~~ theta` to give the equation of motion `ddot theta + (g//L) theta = 0`. By comparison with the simple harmonic motion equation, `ddot theta + omega_0^2 theta = 0`, we can see that the frequency of the pendulum is given by `f = omega_0//2 pi = (1//2 pi)sqrt(g//L)`.
This shows that for small angles of swing, the period of a pendulum is independant of its amplitude. However, when the pendulum swings to larger amplitudes this is no longer the case. Consider the power series expansion for sine:
`sin theta = theta - (theta^3)/(3!) + (theta^5)/(5!) - ...`
The small angles approximation used above keeps just the first term of this expansion. Including the next term as well gives:
`ddot theta + omega_0^2 (theta - (theta^3)/6 + ldots) = 0`
Assume that `theta` is given approximately by `theta ~~ A sin(omega t)`, where `A` is the swing amplitude in radians. When is is substituted into the equation above we are going to get a term in `sin^3(omega t)`. This can be represented by a Fourier series:
`sin^3 (omega t) = a_1 sin (omega t) + a_2 sin (2 omega t) + ...`
The Fourier coefficients `a_n` are given by
`a_n = 2/pi int_0^pi f(theta) sin(n theta) d theta`
so `a_1 = 2/pi int_0^pi sin^4(omega t) d theta = 2/pi times (3 pi)/8 = 3/4`
Therefore `sin^3(omega t) = (3//4)\ sin(omega t) + ...`. So finally we can find the approximate large-angle equation of motion:
`(d^2[A sin(omega t)])/(dt^2) + omega_0^2 (A sin(omega t) - (A^3 sin^3(omega t))/6 + ... ) = 0`
`=> -A omega^2 sin(omega t) + omega_0^2 (A sin(omega t) - (A^3)/6 (3 sin(omega t))/4 ) ~~ 0`
Cancelling `A\ sin(omega t)`, this gives
`omega^2 ~~ omega_0^2 (1 - (A^2)/8 )`
To find the effect on the period, note that `T = (2 pi)/omega`, so (using the binomial expansion)
`T ~~ T_0 (1 - (A^2)/8 )^(-1/2) ~~ T_0 ( 1 + (A^2)/16 )`
So the period is actually `1+(A^2//16)` times longer than the 'ideal' small-angle pendulum's period. If, say, A = 0.05 rad (±50mm at 1m from pivot) the fractional change `Delta T//T_0` is about 13 seconds per day.